Privacy Preserving Data Mining (PPDM) Techniques
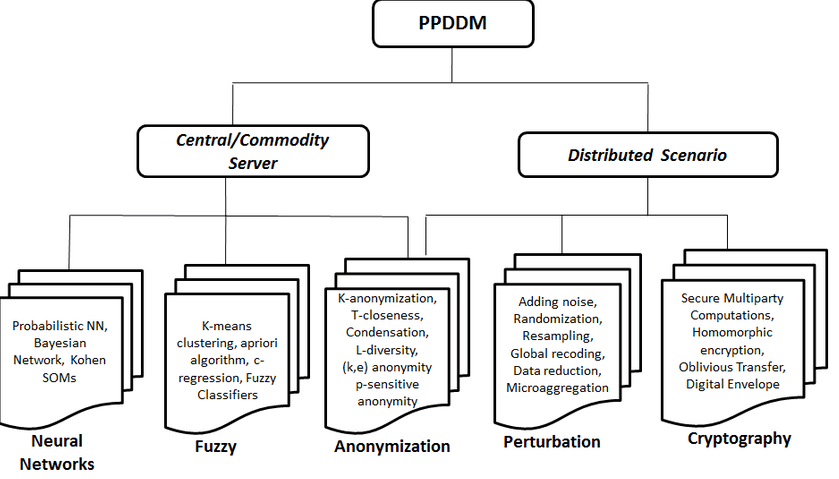
Based on the five dimensions explained in the previous blog different PPDM techniques can be categorized into following categories. PPDM is divided into two parts centralized and distributed which is further categorized into 5 techniques.
1. Anonymization Based:
Anonymization is a technique in which record owner’s identity or sensitive data remain hidden. In a table, the most basic form of data consists of four types of attributes.
It assumes that sensitive data should be retained for research analysis. When micro-data is released for research, with maximizing data utility one must limit disclosure risk to an acceptable level. Undoubtedly, explicit identifiers should be removed but privacy violation is still there as quasi-identifiers are linked to publicly available data. Such attacks are called linkage attacks. For example, attributes such as age, gender, and zip code are available in voter registration list and also available in micro-data, when they linked together, the identity of the individual can be inferred easily
Sensitive data in micro-data is a disease. Quasi-identifiers age, gender, zip code is available both in micro-data as well as voter registration list that is publicly available as shown in Table 1.1 and Table 1.2. So, to limit disclosure risk Sweeney and Samarati proposed the notion of k-anonymity. Sweeney introduced k-anonymity privacy model using generalization and suppression for data anonymization, which requires each record in the anonymized table to be indistinguishable with at least k-1 other records with respect to quasi-identifier attribute in the anonymized dataset.
Table 1: MICRODATA
| ID | AGE | GENDER | ZIP CODE | DISEASE |
| 1 | 25 | MALE | 73661 | COUGH |
| 2 | 27 | MALE | 73634 | COUGH |
| 3 | 31 | MALE | 63967 | FEVER |
| 4 | 39 | FEMALE | 63949 | TOOTHACHE |
Table 2: VOTERS REGISTRATION LIST
| ID | NAME | AGE | GENDER | ZIP CODE |
| 1 | TOM | 25 | MALE | 73661 |
| 2 | LILY | 27 | MALE | 73634 |
| 3 | RAM | 31 | MALE | 63967 |
| 4 | KIM | 39 | FEMALE | 63949 |
The attributes are generalized to a range in order to diminish the granularity of representation and suppression involves deleting or suppresses the data values.
As the name generalization states, the method of generalizing attributes is generalizing values by hierarchies into value which ranges from the minimum to the maximum value of the attribute and form all tuples in same level much alike
If one record in the table has some value Q1, at least k− 1 other records also have the value Q1. In other words, the minimum group size on QID is at least k. A table satisfying this requirement is called k-anonymous. Table3.3 shows an example of 2-anonymous for Table3.1.
Table3: 2-ANONYMOUS TABLE
| ID | AGE | GENDER | ZIP CODE | DISEASE |
| 1 | 2* | MALE | 736* | COUGH |
| 2 | 2* | MALE | 736* | COUGH |
| 3 | 3* | * | 639* | FEVER |
| 4 | 3* | * | 639* | TOOTHACHE |
Even with the voter registration list, a foe can only deduce that Tom may be the person entailed in the first 2 tuples of Table1, or correspondingly, the disease of Tom is uncovered only with probability 50%. In general, k-anonymity give assurance that an individual can be related with his real tuple with a probability no more than 1/k . This reduces the risk of identification when amalgamating with public records while decreases the perfection and data utility of applications on the transformed data. A number of algorithms have been proposed to implement k-anonymity using generalization and suppression. While it ensures that transformed data is true but at the same time it suffers from following:
- High information loss
- Homogeneity and Background Attack
Moreover, limitation of k-anonymity stem from two assumptions: First, it could be very tough for the owner of the database to determine which of the attributes are present and which are not present in external tables. Second, k-anonymity model considers a certain approach of attack, while in real situations there is no justification that why the attacker should not try other approaches.
2. Randomized Response
This technique has been conventionally used in the context of distorting data by probability distribution for methods such as a survey. The method of randomization can be described as follows:
Consider a set of data records denoted by A = {a1…aN}.
For record aiϵ A, a noise component is added which is obtained from the probability distribution fB (b).
The noise components obtained independently of data, and are represented as b1 . . . bN. Hence, the new set of distorted records is represented by a1 +b1 . . . aN +bN. We represent this new set of records by c1 . . . cN. Normally, the assumption taken that the variance of the noise added is in abundant so that the original record values cannot be easily judged from the distorted data. Thus, the original values cannot be retrieved, but the distribution of the original record values can be retrieved. Thus, if A is the random variable representing the data distribution for the original record, B is the random variable representing the noise distribution, and C is the random variable representing the final record, then we have:
C = A + B
A = C – B
Now, we note that N representations of the probability distribution C are known, whereas the distribution B is known publicly. For a number of values of N which are large enough, the probability distribution C can be estimated by deploying numerous methods such as kernel density estimation. By subtracting B from the approximated distribution of C, it is possible to approximate the original probability distribution A. In practice, one can combine the process of approximation of C by subtracting the distribution B from C using numerous iterative methods. Such iterative methods usually have a higher accuracy than the sequential solution of first approximating C and then subtracting B from it. The randomized technique is introduced by Warner in 1965 to solve survey problems. In Randomized response, the data is in such a form that the central place cannot tell with probabilities better than a pre-defined threshold whether the data from a customer contain truthful information or false information. However, information from each individual is disordered, if the number of users is notably large, then the whole information of these users can be estimated with proper accuracy. Such property is useful for decision-tree classification since decision-tree classification is based on aggregate values of a data set, rather than individual data items. Warner solves the following survey problem through randomized response: to make the estimation of the percentage of people in a population having attribute A, queries are sent to a set of people. Since the attribute A is associated with some personal aspects of human life, people may decide either not to reply at all or to reply with wrong answers. Two models: Related-Question Model and Unrelated-Question Model have been proposed to solve this survey problem. In the Related-Question Model, instead of asking each person whether they have to attribute A the interviewer asks each person two related questions, the answers to which are opposing each other. The process of collection of data in Randomized response technique is carried out in two steps: The first step in which data providers randomize their data and send the randomized data to the data receiver. In the second step, the data receiver evaluates the original distribution of the data by using a distribution reconstruction algorithm.
Advantages of response model are:
- Noise is independent of data
- Do not need entire dataset for perturbation
- Can be applied to data collection time
- Does not require a trusted server with all the records
- Very simple and does not require knowledge of distributions of other records in data.
3. CRYPTOGRAPHY BASED
Consider a situation where multiple medical institutions want to conduct a combined research for some benefits without disclosing unnecessary information. In this situation, research regarding symptoms, diagnosis, and medication based on various parameters is to be conducted and at the same time, the privacy of the individuals is to be protected. Such situations are referred to as distributed computing scenarios. The parties involved in such type of task may be competitors or not trusted parties, so privacy becomes the main concern. Cryptographic techniques are preferably implied in such situations where multiple parties work jointly to assess results or share nonsensitive mining results and thereby avoiding revealing of sensitive information. Cryptographic techniques find its usefulness in such situations because of two reasons: First, it provides a well-defined model for privacy that involves methods for quantifying and proving it. Second, a broad set of cryptographic algorithms are available to implement privacy preserving data mining algorithms in this domain. The data may be distributed either horizontally or vertically. Horizontal distribution refers to cases where different records reside in different sites and vertical distribution refers to cases where all values for different attributes reside in different places. Vaidya and Clifton developed a Naive Bayes classifier for preserving privacy on vertically partitioned data. Vaidya and Clifton in proposed a method for clustering over vertically partitioned data. All these methods are based on an encryption protocol is known as Secure Multiparty Computation (SMC) technology. SMC defines two basic adversarial models namely (i) Semi-Honest model and (ii) Malicious model. Semi-honest model follows protocols honestly but can try to deduce the secret information of other parties. In the Malicious model, malicious adversaries can do anything to infer secret information.
Undoubtedly, this approach ensures that transformed data is accurate and secure but this approach fails when more than two parties are involved. Also, the final mining results may lead too privacy loss of individual records.
4.Perturbation Based
In perturbation, the actual record values are exchanged with few substituted data values so that the statistical information evaluated from the perturbed data does not differ from the statistical information computed from the actual data. In perturbation approach, records released is substituted i.e. it does not match to real-world entities represented by the actual data. The perturbed data records do not correlate to real-world record owners; thus, an attacker cannot recover sensitive information from the published data or perform the sensitive linkages. Since only statistical properties of the records are retained, therefore, perturbed data which contains the individual records are meaningless to the recipient. Perturbation can be done by using data swapping or additive noise or synthetic data generation. Since in perturbation technique, rather than reconstructing the original values only the distributions are reconstructed. Hence, new algorithms should be developed which utilize these reconstructed distributions in order to execute mining on the data. So, in this way for each individual data problem such as association rule mining, clustering, or classification, a new distribution based data mining algorithm needs to be developed. For example: For the classification problem a new distribution-based data mining algorithm has been developed by Agrawal.
In perturbation, distribution based data mining algorithm works under an implicit assumption to treat each dimension independently i.e. they treat the distribution of each data dimension reconstructed independently. Pertinent information for data mining algorithms such as classification remains concealed in inter-attribute correlations. For example, the classification technique makes use of a distribution-based analog of single attribute split algorithm. However, other techniques such as multivariate decision tree algorithms cannot be modified accordingly to work with the perturbation approach. Hence the distribution based data mining algorithms have an intrinsic drawback of loss of information present in multidimensional logs.
5. Condensation Based
Condensation technique constructs constrained clusters in the dataset and then produces pseudo-data from the statistics of these clusters. This technique is called condensation as it generates pseudo-data by using condensed statistics of the clusters. It creates groups of non-homogeneous size from the data, such that it is guaranteed that each record lies in a group whose size is at least equal to its anonymity level. This technique uses a procedure which condenses the data into numerous groups of predefined size, for each group, certain statistics are maintained. Each group has a size no less than k, which is referred to as the level of that privacy-preserving approach. As the level increases, the amount of privacy also increases. Simultaneously, a large amount of information loss is there as it involves the condensation of a larger number of records into a single statistical group entity. We use the statistics from each group in order to generate the corresponding pseudo-data. This approach has a number of advantages over other techniques as:
- This technique uses pseudo-data rather than modifications of original data, which helps in the better preservation of privacy.
- There is no need to redesign the data mining algorithms since pseudo data is having the same format as of original data.
But at the same time, data mining results get affected as a large amount of information loss is there because of the condensation of a larger number of records into a single statistical group entity.